다목적 최적설계: 상충하는 설계기준을 다루는 기술
2006-04-03
김일용 : iykim106
- 10812
- 0
1. 머리말
공학설계의 목적은 주어진 제한 조건을 만족시키면서 최대의 성능을 가지는 시스템을 설계하는 것이다. 최근에 컴퓨터의 성능이 비약적으로 발전하고 컴퓨터를 이용한 해석기술 및 도구가 개발됨에 따라, 적은 시간과 비용으로 최고의 성능을 가지는 설계해를 구하는 방법인 최적설계가 활발히 연구되고 있으며 그 활용범위는 산업계의 다양한 분야에서 급격히 증가하는 추세에 있다.
최적설계에서 문제를 정의하는 세 가지 요소는 다음과 같다:
(1) 최대화 또는 최소화 시키고자 하는 성능지수인 “목적함수(objective functions)”
(2) 최종 제품이 만족시켜야 할 설계 제한 조건인 “제한 조건(constraints)”
(3) 설계자가 성능을 향상시키고 제한조건을 만족시키기 위해 변경할 수 있는 설계인자인 “설계변수(design variables)”
목적함수와 제한조건이 설계변수의 함수로 표현될 때, 제한조건을 만족시키면서 최선의 목적함수값을 가지는 설계변수를 체계적으로 찾아내는 방법이 최적설계 방법이다.
공학에서의 최적설계 방법은 크게 두 부류로 나누어 진다. 첫번째는 목적함수나 제한조건의 설계변수에 대한 미분값을 이용하여 최적화를 수행하는 방법인 민감도기반 방법(gradient-based method)으로써 SQP(Sequential Quadratic Programming), Conjugate Gradient Method등이 있다. 다른 종류의 방법은 미분값을 이용하지 않고 경험과 임의성에 근거한 규칙에 의해 설계를 단계적으로 향상시켜 나가는 방법(Heuristic Methods)으로써 유전 알고리즘(Genetic Algorithm), Simulated Annealing등이 있으며 최근에는 무리를 지어 날아가는 새가 먹이를 찾는 방법을 모사한 Particle Swarm Method가 개발되었다.
2. 다목적 최적설계
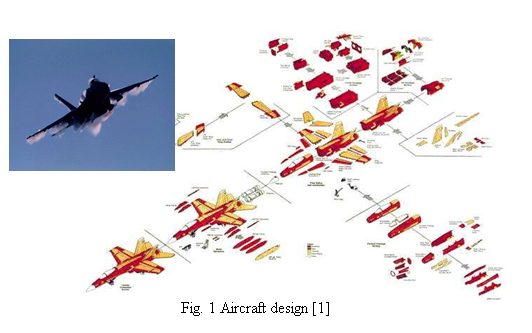
단순한 부품의 최적설계에서는 한 개의 목적함수를 가지도록 설계문제를 정의할 수도 있겠지만, 설계 대상이 조립품(assemblies)이나 시스템(complex systems)으로 점점 복잡해지면 고려되어야 하는 성능지수(목적함수)가 더 많아지게 된다. 한 번에 여러 개의 목적함수를 동시에 최적화하는 것을 다목적 최적설계라 하며, 한 예로써 비행기 시스템 설계에서 고려해야 할 목적함수의 일부는 다음과 같다.
maximize {Range}
maximize {Passenger volume}
maximize {Payload mass}
minimize {Specific fuel consumption}
maximize {Cruise speed}
minimize {Lifecycle cost}
 대부분의 공학시스템 설계의 경우에, 모든 목적함수를 설계자가 원하는 대로 최소화 또는 최대화하는 한 개의 최적해는 존재하지 않으며 목적함수간에 서로 ‘상충(conflict)’하는 경우가 생기게 된다. 앞에서 예로 든 비행기 설계의 경우 일반적으로 유료하중(payload mass)을 증가시키면 연료소비(specific fuel consumption)가 커지게 되며, 항속거리(range)의 증가는 비용(lifecycle cost)의 증가를 수반한다. 이와 같은 특성 때문에 다목적 최적설계의 경우에는 한 개의 최적해가 아니라 여러 개의 최적해가 존재하게 되며, 이 해의 집합은 목적함수공간(성능지수 공간)에서 최선의 트레이드오프 곡면(trade-off surface)를 이루게 된다.
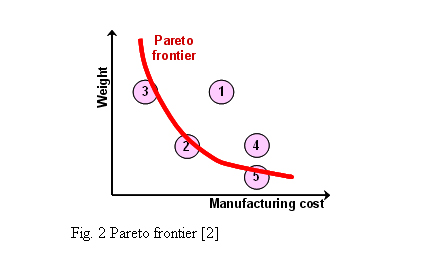
그림 2는 트레이드오프 곡면을 설명하는 간단한 예로써, 두 개의 목적함수(무게, 생산비용)를 동시에 최소화하고자 하는 경우에 다섯 가지 설계후보의 성능을 목적함수 공간에서 보여준다.
설계 후보 1번과 2번을 비교하면 무게와 생산비용에서 2번이 우수하다. 그렇지만 2번과 3번을 비교하면 경량화 측면에서는 2번이 우수하지만 비용측면에서는 3번이 더 우수하기 때문에, 어느 한 쪽이 더 좋다고 말할 수 없다. 다목적 최적설계는 가장 우수한 설계후보의 집합을 찾으며, 이 해의 집합을 파레토 최적해(Pareto optimal solutions)라고 한다. 목적함수 공간에서 이 최적의 설계해들은 곡선(두 개의 목적함수인 경우), 곡면(세 개의 목적함수인 경우), 또는 초곡면(hypersurface, 네 개 이상의 목적함수인 경우)을 이루게 되며 이를 파레토 최적해 표면(Pareto frontier)이라고 한다. 그림 2에서는 설계후보 3번, 2번, 5번을 잇는 곡선이 파레토 최적해 표면을 근사 한다.
대부분의 공학시스템 설계의 경우에, 모든 목적함수를 설계자가 원하는 대로 최소화 또는 최대화하는 한 개의 최적해는 존재하지 않으며 목적함수간에 서로 ‘상충(conflict)’하는 경우가 생기게 된다. 앞에서 예로 든 비행기 설계의 경우 일반적으로 유료하중(payload mass)을 증가시키면 연료소비(specific fuel consumption)가 커지게 되며, 항속거리(range)의 증가는 비용(lifecycle cost)의 증가를 수반한다. 이와 같은 특성 때문에 다목적 최적설계의 경우에는 한 개의 최적해가 아니라 여러 개의 최적해가 존재하게 되며, 이 해의 집합은 목적함수공간(성능지수 공간)에서 최선의 트레이드오프 곡면(trade-off surface)를 이루게 된다.
그림 2는 트레이드오프 곡면을 설명하는 간단한 예로써, 두 개의 목적함수(무게, 생산비용)를 동시에 최소화하고자 하는 경우에 다섯 가지 설계후보의 성능을 목적함수 공간에서 보여준다.
설계 후보 1번과 2번을 비교하면 무게와 생산비용에서 2번이 우수하다. 그렇지만 2번과 3번을 비교하면 경량화 측면에서는 2번이 우수하지만 비용측면에서는 3번이 더 우수하기 때문에, 어느 한 쪽이 더 좋다고 말할 수 없다. 다목적 최적설계는 가장 우수한 설계후보의 집합을 찾으며, 이 해의 집합을 파레토 최적해(Pareto optimal solutions)라고 한다. 목적함수 공간에서 이 최적의 설계해들은 곡선(두 개의 목적함수인 경우), 곡면(세 개의 목적함수인 경우), 또는 초곡면(hypersurface, 네 개 이상의 목적함수인 경우)을 이루게 되며 이를 파레토 최적해 표면(Pareto frontier)이라고 한다. 그림 2에서는 설계후보 3번, 2번, 5번을 잇는 곡선이 파레토 최적해 표면을 근사 한다.
 3. 다목적 최적설계 방법과 응용사례
가중치법(Weighted Sum Method)은 가장 널리 사용되는 다목적 최적설계 방법으로써, 개념이 매우 간단하고 구현이 쉽다. 그러나 일반적으로 파레토 해의 분포가 매우 불균일하고 파레토 최적해 표면이 볼록(convex)하지 않은 경우에는 모든 해를 찾을 수 없는 단점이 있다. 이와 같은 결점을 극복하기 위해서 법선경계교차 방법(NBI: Normal Boundary Intersection Method) 등의 여러 가지 개선된 방법이 제안되었으며, 최근에는 가중치법을 목적함수 공간에서 필요에 따라 선택적으로 적용하는 적응가중치법(AWS: Adaptive Weighted Sum Method)이 개발되었다.
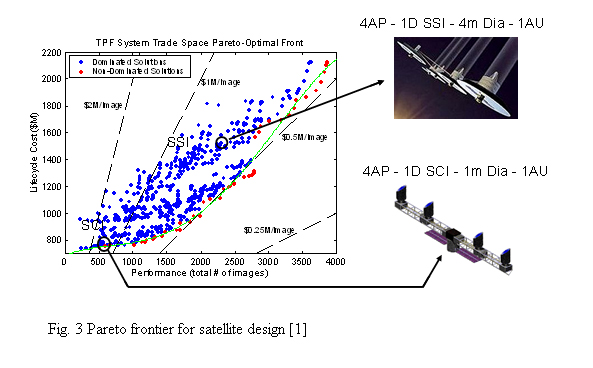
다목적 최적설계는 조립품이나 시스템의 설계뿐 아니라 단품의 설계에서도 사용되며, 인공위성이나 항공기 등의 항공우주 분야, 자동차 분야, 공작기계 분야, 미소기전집적시스템(MEMS: Micro-Electro-Mechanical Systems) 등에서 광범위하게 활용되고 있다. 최근에는 단순 기계부품의 설계에도 기계적인 성능과 생산비용을 동시에 고려하는 연구가 진행되고 있다. 그림 3은 MIT에서 비용과 성능을 목적함수로 하여 인공위성 개발을 위한 다목적 최적설계를 수행한 결과이다.
3. 다목적 최적설계 방법과 응용사례
가중치법(Weighted Sum Method)은 가장 널리 사용되는 다목적 최적설계 방법으로써, 개념이 매우 간단하고 구현이 쉽다. 그러나 일반적으로 파레토 해의 분포가 매우 불균일하고 파레토 최적해 표면이 볼록(convex)하지 않은 경우에는 모든 해를 찾을 수 없는 단점이 있다. 이와 같은 결점을 극복하기 위해서 법선경계교차 방법(NBI: Normal Boundary Intersection Method) 등의 여러 가지 개선된 방법이 제안되었으며, 최근에는 가중치법을 목적함수 공간에서 필요에 따라 선택적으로 적용하는 적응가중치법(AWS: Adaptive Weighted Sum Method)이 개발되었다.
다목적 최적설계는 조립품이나 시스템의 설계뿐 아니라 단품의 설계에서도 사용되며, 인공위성이나 항공기 등의 항공우주 분야, 자동차 분야, 공작기계 분야, 미소기전집적시스템(MEMS: Micro-Electro-Mechanical Systems) 등에서 광범위하게 활용되고 있다. 최근에는 단순 기계부품의 설계에도 기계적인 성능과 생산비용을 동시에 고려하는 연구가 진행되고 있다. 그림 3은 MIT에서 비용과 성능을 목적함수로 하여 인공위성 개발을 위한 다목적 최적설계를 수행한 결과이다.
 4. 다목적 최적설계와 다분야 최적설계
다목적 최적설계(Multiobjective optimization)는 한 개 이상의 목적함수를 고려하여 최적해 집합인 파레토 최적해를 구하는 방법이다. 이와는 다른 개념으로, 최적화 과정에서 목적함수나 제한조건을 평가하기 위하여 여러 가지 학문 분야(discipline)를 동시에 고려하는 경우를 다분야 최적설계(Multidisciplinary optimization)라 한다. 예를 들면, 자동차용 기계 부품을 설계할 때 무게와 최대 응력을 모두 최소화하고자 하는 경우는 목적함수가 두 개이므로 다목적 최적설계이다. 그러나 목적함수나 제한조건의 계산을 위해서 구조해석분야의 이론이나 해석도구만 필요하기 때문에 다분야 최적설계는 아니다.
일반적으로 설계하고자 하는 대상이 단품에서 시스템(complex systems)으로 점점 복잡해짐에 따라 여러 개의 목적함수와 여러 가지의 학문분야를 동시에 고려해야 할 필요성이 점점 커지며 이는 다목적/다분야 최적설계(multiobjective multidisciplinary optimization)문제가 된다. 대표적인 다목적/다분야 최적설계 예는 항공우주 시스템이다. 통신용 인공위성의 설계 시에는 개발/운용 비용(cost), 신뢰성(reliability), 무게(weight), 데이터 처리능력(data rate) 등의 목적 함수를 고려해야 하며, 천체역학(astrodynamics), 열역학(thermodynamics), 통신이론(communications), 광학(optics), 구조해석(structures), 제어(guidance and control) 등의 분야가 포함된다.
5. 맺음말
최적설계기술은 전통적으로 단일 목적함수를 가지는 문제에 많이 적용되어 왔다. 그러나 실제 공학시스템의 설계 시에는 일반적으로 고려해야 할 성능지수(performance measure)가 여러 개 있으며, 이와 같은 문제를 강제로 단일 목적함수 최적설계(single objective optimization)문제로 바꾸기 위해서는 가장 중요한 성능지수를 한 개 선택하거나 각 성능지수의 상대적인 가중치를 미리 결정해야 한다. 다목적 최적설계는 이와 같은 결정을 미리 할 필요 없이 모든 목적함수에 대하여 동시에 최적화를 수행한다. 결과는 단일 최적해가 아니라 최적의 해 집합인 파레토 최적해 표면이 되고, 설계자/정책결정자는 각 성능지수간의 최선의 트레이드오프 곡면을 고려하여 주어진 상황에서 최선의 결정을 내리게 된다.
다목적 최적설계에서는 목적함수의 개수가 증가함에 따라 컴퓨터 계산량이 급격히 늘어나고, 설계하고자 하는 대상이 복잡해지거나 많은 해석분야(multidisciplinary analysis)를 포함할수록 일반적으로 해 집합인 파레토 최적해공간이 불규칙한 모양을 가지게 된다. 기존의 방법으로는 이와 같은 복잡한 문제를 효율적으로 풀 수 없기 때문에 미국/캐나다/유럽 등에서 많은 연구가 수행되고 있으며, 가까운 미래에 더 많은 공학분야의 실용적인 설계문제에 적용되어 성능향상과 비용절감에 크게 도움이 될 것으로 기대한다.
참고문헌
[1] Olivier de Weck and Karen Willcox, MSDO: Multidisciplinary System Design Optimization, Lecture note, MIT, 2004.
[2] Il Yong Kim, Computer Aided Design, Lecture note, Queen’s University, 2005.
[3] Il Yong Kim and Olivier de Weck, “Adaptive Weighted Sum Method for Bi-objective Optimization“, Structural and Multidisciplinary Optimization,” Vol. 29, pp. 149 – 158, 2005.
[4] Il Yong Kim and Olivier de Weck, “Variable Chromosome Length Genetic Algorithm for Progressive Refinement in Topology Optimization,” Structural and Multidisciplinary Optimization, Vol. 29, pp. 445-456, 2005.
[5] Olivier de Weck, “Multiobjective Optimization: History and Promise”, Invited Keynote Paper, GL2-2, The Third China-Japan-Korea Joint Symposium on Optimization of Structural and Mechanical Systems, Kanazawa, Japan, October 30-November 2, 2004.
[6] J. Kennedy and R. Eberhart, “Particle Swarm Optimization,” Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, pp. 1942-1945, 1995.
[7] I. Das and J. E. Dennis, “Normal-Boundary Intersection: A New Method for Generating Pareto Optimal Points in Multicriteria Optimization Problems,” SIAM Journal on Optimization, Vol. 8, pp. 631-657, 1998.
4. 다목적 최적설계와 다분야 최적설계
다목적 최적설계(Multiobjective optimization)는 한 개 이상의 목적함수를 고려하여 최적해 집합인 파레토 최적해를 구하는 방법이다. 이와는 다른 개념으로, 최적화 과정에서 목적함수나 제한조건을 평가하기 위하여 여러 가지 학문 분야(discipline)를 동시에 고려하는 경우를 다분야 최적설계(Multidisciplinary optimization)라 한다. 예를 들면, 자동차용 기계 부품을 설계할 때 무게와 최대 응력을 모두 최소화하고자 하는 경우는 목적함수가 두 개이므로 다목적 최적설계이다. 그러나 목적함수나 제한조건의 계산을 위해서 구조해석분야의 이론이나 해석도구만 필요하기 때문에 다분야 최적설계는 아니다.
일반적으로 설계하고자 하는 대상이 단품에서 시스템(complex systems)으로 점점 복잡해짐에 따라 여러 개의 목적함수와 여러 가지의 학문분야를 동시에 고려해야 할 필요성이 점점 커지며 이는 다목적/다분야 최적설계(multiobjective multidisciplinary optimization)문제가 된다. 대표적인 다목적/다분야 최적설계 예는 항공우주 시스템이다. 통신용 인공위성의 설계 시에는 개발/운용 비용(cost), 신뢰성(reliability), 무게(weight), 데이터 처리능력(data rate) 등의 목적 함수를 고려해야 하며, 천체역학(astrodynamics), 열역학(thermodynamics), 통신이론(communications), 광학(optics), 구조해석(structures), 제어(guidance and control) 등의 분야가 포함된다.
5. 맺음말
최적설계기술은 전통적으로 단일 목적함수를 가지는 문제에 많이 적용되어 왔다. 그러나 실제 공학시스템의 설계 시에는 일반적으로 고려해야 할 성능지수(performance measure)가 여러 개 있으며, 이와 같은 문제를 강제로 단일 목적함수 최적설계(single objective optimization)문제로 바꾸기 위해서는 가장 중요한 성능지수를 한 개 선택하거나 각 성능지수의 상대적인 가중치를 미리 결정해야 한다. 다목적 최적설계는 이와 같은 결정을 미리 할 필요 없이 모든 목적함수에 대하여 동시에 최적화를 수행한다. 결과는 단일 최적해가 아니라 최적의 해 집합인 파레토 최적해 표면이 되고, 설계자/정책결정자는 각 성능지수간의 최선의 트레이드오프 곡면을 고려하여 주어진 상황에서 최선의 결정을 내리게 된다.
다목적 최적설계에서는 목적함수의 개수가 증가함에 따라 컴퓨터 계산량이 급격히 늘어나고, 설계하고자 하는 대상이 복잡해지거나 많은 해석분야(multidisciplinary analysis)를 포함할수록 일반적으로 해 집합인 파레토 최적해공간이 불규칙한 모양을 가지게 된다. 기존의 방법으로는 이와 같은 복잡한 문제를 효율적으로 풀 수 없기 때문에 미국/캐나다/유럽 등에서 많은 연구가 수행되고 있으며, 가까운 미래에 더 많은 공학분야의 실용적인 설계문제에 적용되어 성능향상과 비용절감에 크게 도움이 될 것으로 기대한다.
참고문헌
[1] Olivier de Weck and Karen Willcox, MSDO: Multidisciplinary System Design Optimization, Lecture note, MIT, 2004.
[2] Il Yong Kim, Computer Aided Design, Lecture note, Queen’s University, 2005.
[3] Il Yong Kim and Olivier de Weck, “Adaptive Weighted Sum Method for Bi-objective Optimization“, Structural and Multidisciplinary Optimization,” Vol. 29, pp. 149 – 158, 2005.
[4] Il Yong Kim and Olivier de Weck, “Variable Chromosome Length Genetic Algorithm for Progressive Refinement in Topology Optimization,” Structural and Multidisciplinary Optimization, Vol. 29, pp. 445-456, 2005.
[5] Olivier de Weck, “Multiobjective Optimization: History and Promise”, Invited Keynote Paper, GL2-2, The Third China-Japan-Korea Joint Symposium on Optimization of Structural and Mechanical Systems, Kanazawa, Japan, October 30-November 2, 2004.
[6] J. Kennedy and R. Eberhart, “Particle Swarm Optimization,” Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, pp. 1942-1945, 1995.
[7] I. Das and J. E. Dennis, “Normal-Boundary Intersection: A New Method for Generating Pareto Optimal Points in Multicriteria Optimization Problems,” SIAM Journal on Optimization, Vol. 8, pp. 631-657, 1998.
 대부분의 공학시스템 설계의 경우에, 모든 목적함수를 설계자가 원하는 대로 최소화 또는 최대화하는 한 개의 최적해는 존재하지 않으며 목적함수간에 서로 ‘상충(conflict)’하는 경우가 생기게 된다. 앞에서 예로 든 비행기 설계의 경우 일반적으로 유료하중(payload mass)을 증가시키면 연료소비(specific fuel consumption)가 커지게 되며, 항속거리(range)의 증가는 비용(lifecycle cost)의 증가를 수반한다. 이와 같은 특성 때문에 다목적 최적설계의 경우에는 한 개의 최적해가 아니라 여러 개의 최적해가 존재하게 되며, 이 해의 집합은 목적함수공간(성능지수 공간)에서 최선의 트레이드오프 곡면(trade-off surface)를 이루게 된다.
그림 2는 트레이드오프 곡면을 설명하는 간단한 예로써, 두 개의 목적함수(무게, 생산비용)를 동시에 최소화하고자 하는 경우에 다섯 가지 설계후보의 성능을 목적함수 공간에서 보여준다.
설계 후보 1번과 2번을 비교하면 무게와 생산비용에서 2번이 우수하다. 그렇지만 2번과 3번을 비교하면 경량화 측면에서는 2번이 우수하지만 비용측면에서는 3번이 더 우수하기 때문에, 어느 한 쪽이 더 좋다고 말할 수 없다. 다목적 최적설계는 가장 우수한 설계후보의 집합을 찾으며, 이 해의 집합을 파레토 최적해(Pareto optimal solutions)라고 한다. 목적함수 공간에서 이 최적의 설계해들은 곡선(두 개의 목적함수인 경우), 곡면(세 개의 목적함수인 경우), 또는 초곡면(hypersurface, 네 개 이상의 목적함수인 경우)을 이루게 되며 이를 파레토 최적해 표면(Pareto frontier)이라고 한다. 그림 2에서는 설계후보 3번, 2번, 5번을 잇는 곡선이 파레토 최적해 표면을 근사 한다.
대부분의 공학시스템 설계의 경우에, 모든 목적함수를 설계자가 원하는 대로 최소화 또는 최대화하는 한 개의 최적해는 존재하지 않으며 목적함수간에 서로 ‘상충(conflict)’하는 경우가 생기게 된다. 앞에서 예로 든 비행기 설계의 경우 일반적으로 유료하중(payload mass)을 증가시키면 연료소비(specific fuel consumption)가 커지게 되며, 항속거리(range)의 증가는 비용(lifecycle cost)의 증가를 수반한다. 이와 같은 특성 때문에 다목적 최적설계의 경우에는 한 개의 최적해가 아니라 여러 개의 최적해가 존재하게 되며, 이 해의 집합은 목적함수공간(성능지수 공간)에서 최선의 트레이드오프 곡면(trade-off surface)를 이루게 된다.
그림 2는 트레이드오프 곡면을 설명하는 간단한 예로써, 두 개의 목적함수(무게, 생산비용)를 동시에 최소화하고자 하는 경우에 다섯 가지 설계후보의 성능을 목적함수 공간에서 보여준다.
설계 후보 1번과 2번을 비교하면 무게와 생산비용에서 2번이 우수하다. 그렇지만 2번과 3번을 비교하면 경량화 측면에서는 2번이 우수하지만 비용측면에서는 3번이 더 우수하기 때문에, 어느 한 쪽이 더 좋다고 말할 수 없다. 다목적 최적설계는 가장 우수한 설계후보의 집합을 찾으며, 이 해의 집합을 파레토 최적해(Pareto optimal solutions)라고 한다. 목적함수 공간에서 이 최적의 설계해들은 곡선(두 개의 목적함수인 경우), 곡면(세 개의 목적함수인 경우), 또는 초곡면(hypersurface, 네 개 이상의 목적함수인 경우)을 이루게 되며 이를 파레토 최적해 표면(Pareto frontier)이라고 한다. 그림 2에서는 설계후보 3번, 2번, 5번을 잇는 곡선이 파레토 최적해 표면을 근사 한다.
 3. 다목적 최적설계 방법과 응용사례
가중치법(Weighted Sum Method)은 가장 널리 사용되는 다목적 최적설계 방법으로써, 개념이 매우 간단하고 구현이 쉽다. 그러나 일반적으로 파레토 해의 분포가 매우 불균일하고 파레토 최적해 표면이 볼록(convex)하지 않은 경우에는 모든 해를 찾을 수 없는 단점이 있다. 이와 같은 결점을 극복하기 위해서 법선경계교차 방법(NBI: Normal Boundary Intersection Method) 등의 여러 가지 개선된 방법이 제안되었으며, 최근에는 가중치법을 목적함수 공간에서 필요에 따라 선택적으로 적용하는 적응가중치법(AWS: Adaptive Weighted Sum Method)이 개발되었다.
다목적 최적설계는 조립품이나 시스템의 설계뿐 아니라 단품의 설계에서도 사용되며, 인공위성이나 항공기 등의 항공우주 분야, 자동차 분야, 공작기계 분야, 미소기전집적시스템(MEMS: Micro-Electro-Mechanical Systems) 등에서 광범위하게 활용되고 있다. 최근에는 단순 기계부품의 설계에도 기계적인 성능과 생산비용을 동시에 고려하는 연구가 진행되고 있다. 그림 3은 MIT에서 비용과 성능을 목적함수로 하여 인공위성 개발을 위한 다목적 최적설계를 수행한 결과이다.
3. 다목적 최적설계 방법과 응용사례
가중치법(Weighted Sum Method)은 가장 널리 사용되는 다목적 최적설계 방법으로써, 개념이 매우 간단하고 구현이 쉽다. 그러나 일반적으로 파레토 해의 분포가 매우 불균일하고 파레토 최적해 표면이 볼록(convex)하지 않은 경우에는 모든 해를 찾을 수 없는 단점이 있다. 이와 같은 결점을 극복하기 위해서 법선경계교차 방법(NBI: Normal Boundary Intersection Method) 등의 여러 가지 개선된 방법이 제안되었으며, 최근에는 가중치법을 목적함수 공간에서 필요에 따라 선택적으로 적용하는 적응가중치법(AWS: Adaptive Weighted Sum Method)이 개발되었다.
다목적 최적설계는 조립품이나 시스템의 설계뿐 아니라 단품의 설계에서도 사용되며, 인공위성이나 항공기 등의 항공우주 분야, 자동차 분야, 공작기계 분야, 미소기전집적시스템(MEMS: Micro-Electro-Mechanical Systems) 등에서 광범위하게 활용되고 있다. 최근에는 단순 기계부품의 설계에도 기계적인 성능과 생산비용을 동시에 고려하는 연구가 진행되고 있다. 그림 3은 MIT에서 비용과 성능을 목적함수로 하여 인공위성 개발을 위한 다목적 최적설계를 수행한 결과이다.
 4. 다목적 최적설계와 다분야 최적설계
다목적 최적설계(Multiobjective optimization)는 한 개 이상의 목적함수를 고려하여 최적해 집합인 파레토 최적해를 구하는 방법이다. 이와는 다른 개념으로, 최적화 과정에서 목적함수나 제한조건을 평가하기 위하여 여러 가지 학문 분야(discipline)를 동시에 고려하는 경우를 다분야 최적설계(Multidisciplinary optimization)라 한다. 예를 들면, 자동차용 기계 부품을 설계할 때 무게와 최대 응력을 모두 최소화하고자 하는 경우는 목적함수가 두 개이므로 다목적 최적설계이다. 그러나 목적함수나 제한조건의 계산을 위해서 구조해석분야의 이론이나 해석도구만 필요하기 때문에 다분야 최적설계는 아니다.
일반적으로 설계하고자 하는 대상이 단품에서 시스템(complex systems)으로 점점 복잡해짐에 따라 여러 개의 목적함수와 여러 가지의 학문분야를 동시에 고려해야 할 필요성이 점점 커지며 이는 다목적/다분야 최적설계(multiobjective multidisciplinary optimization)문제가 된다. 대표적인 다목적/다분야 최적설계 예는 항공우주 시스템이다. 통신용 인공위성의 설계 시에는 개발/운용 비용(cost), 신뢰성(reliability), 무게(weight), 데이터 처리능력(data rate) 등의 목적 함수를 고려해야 하며, 천체역학(astrodynamics), 열역학(thermodynamics), 통신이론(communications), 광학(optics), 구조해석(structures), 제어(guidance and control) 등의 분야가 포함된다.
5. 맺음말
최적설계기술은 전통적으로 단일 목적함수를 가지는 문제에 많이 적용되어 왔다. 그러나 실제 공학시스템의 설계 시에는 일반적으로 고려해야 할 성능지수(performance measure)가 여러 개 있으며, 이와 같은 문제를 강제로 단일 목적함수 최적설계(single objective optimization)문제로 바꾸기 위해서는 가장 중요한 성능지수를 한 개 선택하거나 각 성능지수의 상대적인 가중치를 미리 결정해야 한다. 다목적 최적설계는 이와 같은 결정을 미리 할 필요 없이 모든 목적함수에 대하여 동시에 최적화를 수행한다. 결과는 단일 최적해가 아니라 최적의 해 집합인 파레토 최적해 표면이 되고, 설계자/정책결정자는 각 성능지수간의 최선의 트레이드오프 곡면을 고려하여 주어진 상황에서 최선의 결정을 내리게 된다.
다목적 최적설계에서는 목적함수의 개수가 증가함에 따라 컴퓨터 계산량이 급격히 늘어나고, 설계하고자 하는 대상이 복잡해지거나 많은 해석분야(multidisciplinary analysis)를 포함할수록 일반적으로 해 집합인 파레토 최적해공간이 불규칙한 모양을 가지게 된다. 기존의 방법으로는 이와 같은 복잡한 문제를 효율적으로 풀 수 없기 때문에 미국/캐나다/유럽 등에서 많은 연구가 수행되고 있으며, 가까운 미래에 더 많은 공학분야의 실용적인 설계문제에 적용되어 성능향상과 비용절감에 크게 도움이 될 것으로 기대한다.
참고문헌
[1] Olivier de Weck and Karen Willcox, MSDO: Multidisciplinary System Design Optimization, Lecture note, MIT, 2004.
[2] Il Yong Kim, Computer Aided Design, Lecture note, Queen’s University, 2005.
[3] Il Yong Kim and Olivier de Weck, “Adaptive Weighted Sum Method for Bi-objective Optimization“, Structural and Multidisciplinary Optimization,” Vol. 29, pp. 149 – 158, 2005.
[4] Il Yong Kim and Olivier de Weck, “Variable Chromosome Length Genetic Algorithm for Progressive Refinement in Topology Optimization,” Structural and Multidisciplinary Optimization, Vol. 29, pp. 445-456, 2005.
[5] Olivier de Weck, “Multiobjective Optimization: History and Promise”, Invited Keynote Paper, GL2-2, The Third China-Japan-Korea Joint Symposium on Optimization of Structural and Mechanical Systems, Kanazawa, Japan, October 30-November 2, 2004.
[6] J. Kennedy and R. Eberhart, “Particle Swarm Optimization,” Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, pp. 1942-1945, 1995.
[7] I. Das and J. E. Dennis, “Normal-Boundary Intersection: A New Method for Generating Pareto Optimal Points in Multicriteria Optimization Problems,” SIAM Journal on Optimization, Vol. 8, pp. 631-657, 1998.
4. 다목적 최적설계와 다분야 최적설계
다목적 최적설계(Multiobjective optimization)는 한 개 이상의 목적함수를 고려하여 최적해 집합인 파레토 최적해를 구하는 방법이다. 이와는 다른 개념으로, 최적화 과정에서 목적함수나 제한조건을 평가하기 위하여 여러 가지 학문 분야(discipline)를 동시에 고려하는 경우를 다분야 최적설계(Multidisciplinary optimization)라 한다. 예를 들면, 자동차용 기계 부품을 설계할 때 무게와 최대 응력을 모두 최소화하고자 하는 경우는 목적함수가 두 개이므로 다목적 최적설계이다. 그러나 목적함수나 제한조건의 계산을 위해서 구조해석분야의 이론이나 해석도구만 필요하기 때문에 다분야 최적설계는 아니다.
일반적으로 설계하고자 하는 대상이 단품에서 시스템(complex systems)으로 점점 복잡해짐에 따라 여러 개의 목적함수와 여러 가지의 학문분야를 동시에 고려해야 할 필요성이 점점 커지며 이는 다목적/다분야 최적설계(multiobjective multidisciplinary optimization)문제가 된다. 대표적인 다목적/다분야 최적설계 예는 항공우주 시스템이다. 통신용 인공위성의 설계 시에는 개발/운용 비용(cost), 신뢰성(reliability), 무게(weight), 데이터 처리능력(data rate) 등의 목적 함수를 고려해야 하며, 천체역학(astrodynamics), 열역학(thermodynamics), 통신이론(communications), 광학(optics), 구조해석(structures), 제어(guidance and control) 등의 분야가 포함된다.
5. 맺음말
최적설계기술은 전통적으로 단일 목적함수를 가지는 문제에 많이 적용되어 왔다. 그러나 실제 공학시스템의 설계 시에는 일반적으로 고려해야 할 성능지수(performance measure)가 여러 개 있으며, 이와 같은 문제를 강제로 단일 목적함수 최적설계(single objective optimization)문제로 바꾸기 위해서는 가장 중요한 성능지수를 한 개 선택하거나 각 성능지수의 상대적인 가중치를 미리 결정해야 한다. 다목적 최적설계는 이와 같은 결정을 미리 할 필요 없이 모든 목적함수에 대하여 동시에 최적화를 수행한다. 결과는 단일 최적해가 아니라 최적의 해 집합인 파레토 최적해 표면이 되고, 설계자/정책결정자는 각 성능지수간의 최선의 트레이드오프 곡면을 고려하여 주어진 상황에서 최선의 결정을 내리게 된다.
다목적 최적설계에서는 목적함수의 개수가 증가함에 따라 컴퓨터 계산량이 급격히 늘어나고, 설계하고자 하는 대상이 복잡해지거나 많은 해석분야(multidisciplinary analysis)를 포함할수록 일반적으로 해 집합인 파레토 최적해공간이 불규칙한 모양을 가지게 된다. 기존의 방법으로는 이와 같은 복잡한 문제를 효율적으로 풀 수 없기 때문에 미국/캐나다/유럽 등에서 많은 연구가 수행되고 있으며, 가까운 미래에 더 많은 공학분야의 실용적인 설계문제에 적용되어 성능향상과 비용절감에 크게 도움이 될 것으로 기대한다.
참고문헌
[1] Olivier de Weck and Karen Willcox, MSDO: Multidisciplinary System Design Optimization, Lecture note, MIT, 2004.
[2] Il Yong Kim, Computer Aided Design, Lecture note, Queen’s University, 2005.
[3] Il Yong Kim and Olivier de Weck, “Adaptive Weighted Sum Method for Bi-objective Optimization“, Structural and Multidisciplinary Optimization,” Vol. 29, pp. 149 – 158, 2005.
[4] Il Yong Kim and Olivier de Weck, “Variable Chromosome Length Genetic Algorithm for Progressive Refinement in Topology Optimization,” Structural and Multidisciplinary Optimization, Vol. 29, pp. 445-456, 2005.
[5] Olivier de Weck, “Multiobjective Optimization: History and Promise”, Invited Keynote Paper, GL2-2, The Third China-Japan-Korea Joint Symposium on Optimization of Structural and Mechanical Systems, Kanazawa, Japan, October 30-November 2, 2004.
[6] J. Kennedy and R. Eberhart, “Particle Swarm Optimization,” Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, pp. 1942-1945, 1995.
[7] I. Das and J. E. Dennis, “Normal-Boundary Intersection: A New Method for Generating Pareto Optimal Points in Multicriteria Optimization Problems,” SIAM Journal on Optimization, Vol. 8, pp. 631-657, 1998.


